2021-05-09 10:58:21 来源:网络发表评论
2020下初中数学教师资格证面试试题及答案【1月10日上午】
初中数学《三角形全等的判定——AAS》
一、考题回顾

二、考题解析
【教学过程】
(一)导入新课
回顾已经学过的三角形全等判定定理及其简称(三边分别相等、两边及其夹角分别相等、两角及其夹边分别相等)与不能判定三角形全等的条件组合(两边及其中一边对角分别相等)。引题:两角和其中一角的对边分别相等能否判定两个三角形全等?板书课题《三角形全等的判定》

(四)小结作业
小结:学生自主总结本节课的收获。
作业:思考——三个角分别相等能否判定三角形全等?直角三角形有没有特殊的全等判定条件?下节课继续学习。
【板书设计】
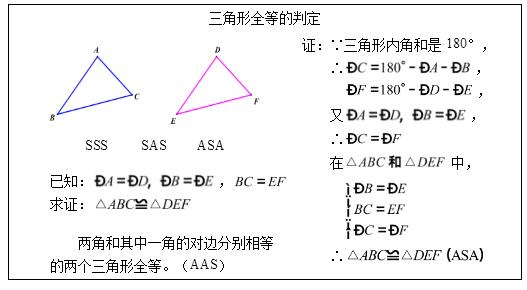
【答辩题目解析】
1.三角形全等的判定方法都有哪些?
【参考答案】
三角形全等的判定方法共有五种,分别如下:
边边边(SSS)——三边分别相等的两个三角形全等;
边角边(SAS)——两边及其夹角分别相等的两个三角形全等;
角边角(ASA)——两角及其夹边分别相等的两个三角形全等;
以上三种判定属于初中数学九个基本事实。
利用“角边角”和三角形的内角和可以推出第四种判定,
角角边(AAS)——两角及其中一角对边分别相等的两个三角形全等;
第五种方法仅适用于两个直角三角形全等的判定,
斜边、直角边(HL)——斜边和一条直角边分别相等的两个直角三角形全等。
2.你是如何设计探究AAS判定定理的?
【参考答案】
AAS判定定理的探究分为猜想和证明两个环节。猜想环节,我设置一个学生活动:给定两角大小及一角对边的长度,让学生动手画符合条件的三角形。首先独立完成,然后四人一组,通过裁剪、重叠,学生发现组内的四个三角形全等;接着我任选几个小组,通过重叠的方式向学生展示大家做出的三角形都全等。经过亲身经历,学生能够得到AAS可以判定三角形全等的猜想。接下来才进行严谨的数学证明,引导学生利用已学过的ASA来证明AAS,渗透转化思想,锻炼知识的迁移能力。
我之所以在题本的基础之上补充动手操作的猜想环节,是因为考虑到学生的认知规律。先通过动手操作感性地认识AAS也许可以判定三角形全等,有了经验支撑,再通过数学证明理性地认知AAS判定定理。这是一个比较完整的探究过程或认知流程。
初中数学《二次函数的应用》
一、考题回顾

二、考题解析
【教学过程】
(一)课堂导入
创设情境导入:屏幕展示靶场场景图,提问靶场上如何瞄准?展示篮球场图片,提问如何投篮才能进?预设学生得到照门缺口、准星、目标三点一线时就能瞄准,投篮出手位置、篮球在空中最高点、篮筐在同一条抛物线时,投篮就比较容易进。直线、抛物线都能解决实际问题,引出课题。
(二)回顾旧知
回顾二次函数解析式的形式及确定解析式的方法——待定系数法。
(三)习题精讲
出示例题:抛物线形拱桥,当拱顶离水面2m时,水面宽4m,水面下降1m,水面宽度增加多少?


2.如何渗透模型思想?
【参考答案】
模型思想作为分析问题、解决问题的思想方法,在教学中需要逐步渗透,帮助学生深刻理解、逐步掌握、灵活运用。
以二次函数为例,在教学中,我首先引导学生认识、理解二次函数的特点,形成充分的感知经验,多维度、多方面地认识基本的二次函数图象及性质;其次在实际问题中注重引导,联系实际运用模型解决问题,本节课正是让学生主动联想已有知识经验,结合动手操作等直接感受,运用二次函数解决问题;最后在经历了一个完整的运用数学模型解决问题的过程后,总结反思模型思想解决问题的便捷性,加深对模型思想的理解。
初中数学《有理数的除法》
一、考题回顾

注:图片节选自人民教育出版社初中数学七年级上册第34页
二、考题解析
【教学过程】
(一)导入新课
简单回顾有理数的乘法法则。
按照四则运算的顺序,引出本节课学习有理数的除法。
(二)讲解新知

(四)小结作业
小结:带领学生简要回顾本节课内容。
作业:完成书上练习题;总结有理数的四则运算法则。
【板书设计】

【答辩题目解析】
1.请简述有理数的四则运算法则。
【参考答案】
有理数加法法则分三条陈述:
①同号两数相加,取相同的符号,并把绝对值相加。
②绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。互为相反数的两个数相加得0。
③一个数同0相加,仍得这个数。
有理数减法法则:减去一个数,等于加这个数的相反数。实际是将减法转化为加法进行计算。
有理数乘法法则:
①两数相乘,同号得正,异号得负,并把绝对值相乘。任何数同0相乘,都得0。
②几个不等于0的数相乘,积的符号由负因数的个数决定。当负因数的个数为奇数时,积为负,当负因数的个数为偶数时,积为正。
③几个数相乘,有一个因数为0,积就为0。
与减法法则类似,有理数除法法则是除以一个不等于0的数,等于乘这个数的倒数。还可以详细描述为:两数相除,同号得正,异号得负,并把绝对值相除。0除以任何一个不等于0的数,都得0。
2.说一说本节课探究有理数除法法则的思路。
【参考答案】

| 中学教资笔试 | 【直通车】2024上中学教资笔面直通车 | ¥5980 | 查看详情 |
| 【无忧班】2024上中学教资笔试无忧协议班 | ¥2480 | 查看详情 | |
| 【联报班】科一+科二+语/数/英/音联报 | ¥293 | 查看详情 | |
| 【全程班】中学教资带背全程班 | ¥199 | 查看详情 | |
| 【单项班】中学教资单项班 | ¥79 | 查看详情 | |
| 【普通话】普通话考试急速提升班 | ¥9.9 | 查看详情 | |
| 小学教资 | 【直通车】2024上 小学教资笔面直通车 | ¥5980 | 查看优惠 |
| 【无忧班】2024上小学教资笔试无忧协议班 | ¥2480 | 查看详情 | |
| 【全程班】小学教资带背全程班 | ¥199 | 查看详情 | |
| 【单项班】小学教资单项班 | ¥99 | 查看详情 | |
| 【普通话】普通话考试急速提升班 | ¥9.9 | 查看详情 |